Cara Kreatif Menentukan Himpunan Penyelesaian Pertidaksamaan Kuadrat

Ujian masuk perguruan tinggi negeri atau penerimaan mahasiswa baru PTN akan segera dilaksanakan. Sebagai persiapan dasar, karena untuk ujian masuk PTN kemampuan kita di dalam menjawab soal sangat dibutuhkan. Istilah orang bimbingan adalah cara cepat, the king, fastes solution atau apalah istilahnya.

Disini istilahnya diberi nama 'matematika kreatif untuk sudut istimewa dan matematika kreatif lainnya lihat [disini]

Pertidaksamaan Kuadrat

Bentuk Umum:

• ❶ $ ax^2 + bx + c \gt 0$
• ❷ $ ax^2 + bx + c \geq 0$
• ❸ $ ax^2 + bx + c \lt 0$
• ❹ $ ax^2 + bx + c \leq 0$

Apa gunanya bentuk umum ini, jika ada soal pertidaksamaan kuadrat ubahlah bentuknya sampai kepada bentuk umum. Kalau sudah sampai pada bentuk umum, lanjutkan ke langkah berikutnya yaitu mencari pembuat nol ruas kiri. Variabel pembuat nol ruas kiri ada dua, kita misalkan nilainya adalah $x = B\ (Besar)$ atau $x = K\ (Kecil)$.

Misal bentuk pertidaksamaan kuadratnya sebagai berikut:

• ❶ $ (x-B)(x-K) \gt 0$ ➨ HP adalah: $ x\ \lt K\ atau\ x\ \gt\ B$
• ❷ $ (x-B)(x-K) \geq 0$ ➨ HP adalah: $ x\ \leq\ K\ atau\ x\ \geq\ B$
• ❸ $ (x-B)(x-K) \lt 0$ ➨ HP adalah: $ K\ \lt\ x\ \lt\ B$
• ❹ $ (x-B)(x-K) \leq 0$ ➨ HP adalah: $ K\ \leq\ x\ \leq\ B$

Mungkin biar lebih pas, mungkin kita lihat dengan contoh, soal berikut tidak murni pertidaksamaan kuadrat tetapi digabung dengan fungsi naik diambil dari soal matematika dasar tes masuk UNPAD tahun 2008.

Alternatif Pembahasan;
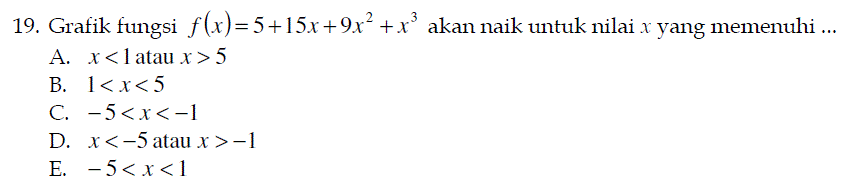
Syarat suatu fungsi akan naik adalah turunan pertama lebih dari nol $f'(x) \gt 0$,
turunan pertama soal adalah $f'(x)=3x^2+18x+15$

$ 3x^2+18x+15 \gt 0$ (*sama dengan bentuk ❶)
$ x^2+6x+5 \gt 0$
$ (x+1)(x+5) \gt 0$
diperoleh $x =-1\ (B)$ atau $x = -5\ (K)$

Kesimpulan:
Himpunan Penyelesaian adalah: $ x \lt -5\ \text{atau}\ x \gt -1$

Jika soal diatas kita kembangkan menjadi pertanyaan kedua yaitu grafik fungsi $f(x)=5+15x+9x^{2}+x^{3}$ akan turun pada nilai $x$ yang memenuhi adalah...

Syarat suatu fungsi akan turun adalah turunan pertama kurang dari nol $f'(x) \lt 0$,
turunan pertama soal adalah $f'(x)=3x^2+18x+15$

$ 3x^2+18x+15 \lt 0$ (*sama dengan bentuk ❸)
$ x^2+6x+5 \lt 0$
$ (x+1)(x+5) \lt 0$
diperoleh $x =-1\ (B)$ atau $x = -5\ (K)$

Kesimpulan:
Himpunan Penyelesaian adalah: $ -5 \lt x \lt -1$

Agar bisa lebih paham lagi, coba dengan soal pertidaksamaan kuadrat yang lainnya, mulai dari bentuk yang paling sederhana.

Kreatifitas diatas mungkin sudah lama Anda ketahui atau Anda punya matematika kreatif bentuk yang lain, tidak ada salahnya kita saling berbagi disini😊CMIIW

Jangan Lupa Untuk Berbagi 🙏Share is Caring 👀 dan JADIKAN HARI INI LUAR BIASA! - WITH GOD ALL THINGS ARE POSSIBLE😊

Kreatifitas dalam mengerjakan soal seperti ini sebaiknya Jangan Anda berikan konsepnya kepada siswa sebelum mereka betul-betul paham konsep pertidaksamaan kuadrat dengan benar. Karena cara kreatif menjawab soal diketahui seseorang ketika dia sudah mengetahui konsep sebenarnya.

Video pilihan khusus untuk Anda 💗 Masih menganggap matematika hanya hitung-hitungan semata, mari kita lihat kreativitas siswa ini;

Sumber https://www.defantri.com/

Bagikan Artikel ini